2.1. Getting started¶
This guide will get you started with DynSem to specify the dynamic semantics of your language. You’ll be guided through:
- Your first DynSem module
- Context-free semantics
- Context-sensitive semantics
- Conditional semantics
- Semantic libraries using meta-functions
- Semantics of functions
- Get ready for interpretation
- Call into Java code
- Run a program
Note
DynSem is actively developed and this guide requires features only available in the bleeding edge DynSem. To follow along this tutorial it’s best to have the latest Spoofax 2.3.0 nightly build installed.
2.1.1. The SIMPL language¶
This guide is centered around a very simple language we call SIMPL. The SIMPL code is kept in a GitHub SIMPL repository. We start with a basic definition (in SDF3) of concrete syntax which covers arithmetic expressions:
1 2 3 4 5 6 7 8 9 | context-free start-symbols
Exp
context-free syntax
Exp.Lit = <<INT>>
Exp.Plus = <<Exp> + <Exp>> {left}
Exp.Minus = <<Exp> - <Exp>> {left}
Exp.Times = <<Exp> * <Exp>> {left}
Exp = <(<Exp>)> {bracket}
|
Note that terms of the sort Exp are start symbols for SIMPL programs.
2.1.2. Your first DynSem module¶
We create the main DynSem module named trans/simpl in the file trans/simpl.ds:
1 2 3 4 | module trans/simpl
imports
src-gen/ds-signatures/simpl-sig
|
The module imports the abstract syntax definitions (term signatures) which is generated from the concrete syntax definition:
1 2 3 4 5 6 7 8 9 10 11 12 | module ds-signatures/simpl-sig
imports ds-signatures/Common-sig
signature
sorts
Exp
constructors
Lit : INT -> Exp
Plus : Exp * Exp -> Exp
Minus : Exp * Exp -> Exp
Times : Exp * Exp -> Exp
|
Importing these makes the sorts and constructors available to the rest of the modules. We extend module trans/simpl with definitions for value sorts and for the main reduction relation:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | module trans/simpl
imports
src-gen/ds-signatures/simpl-sig
signature
sorts
V
constructors
NumV: Int -> V
arrows
Exp --> V
variables
v : V
|
We declared constructor NumV which will be used to represent numerical value terms. We also declare reduction relation Exp --> V from Exp terms to values V, and a variable scheme for variables named v. For details about the signature section of DynSem specification see the Term signatures and Signatures of arrows, components and meta-functions.
2.1.3. Context-free semantics¶
We specify reduction rules for SIMPL constructs that do not depend on the evaluation contexts (such as environments). These are number literals, and simple arithmetic operations. The reduction rules are given in a big-step style:
1 2 3 4 5 6 7 | rules
Lit(s) --> NumV(parseI(s)).
Plus(e1, e2) --> NumV(addI(i1, i2))
where
e1 --> NumV(i1);
e2 --> NumV(i2).
|
The first rule specifies that literal terms such as 42 whose abstract syntax is of the form Lit("42") evaluate to NumV terms. The second rule specifies the semantics of the addition expressions of the form Plus(e1, e2) inductively on the default reduction relation. First the expression e1 is reduced and the expectation is that it reduces to a NumV term. Variable i1 is bound to the integer value surrounded by the resulting NumV term. This is captured in the first premise of the reduction rule. Similarly, the reduction of the right expression of the addition is captured in the second premise. The conclusion of the rule composes the two integers to a NumV term.
In the rules above, parseI and addI are native operators which we provide the functionality of parsing a string into an integer, and of adding two integers, respectively. We provide the signatures for these when we look at Call into Java code.
Note
Dissimilar to regular big-step style rules, premises in DynSem are ordered. The Plus rule above states that the left expression will be evaluated first and the right expression second.
The rules for subtraction and multiplication proceed similarly:
1 2 3 4 5 6 7 8 9 | Minus(e1, e2) --> NumV(subI(i1, i2))
where
e1 --> NumV(i1);
e2 --> NumV(i2).
Times(e1, e2) --> NumV(mulI(i1, i2))
where
e1 --> NumV(i1);
e2 --> NumV(i2).
|
In all three rules seen so far ( Plus, Minus, Times ) the reductions for the subexpressions can be specified implicitly:
1 2 3 | Plus(NumV(i1), NumV(i2)) --> NumV(addI(i1, i2)).
Minus(NumV(i1), NumV(i2)) --> NumV(subI(i1, i2)).
Times(NumV(i1), NumV(i2)) --> NumV(mulI(i1, i2)).
|
Specifying the reductions and term expectations implicitly allows rules to be written more concisely without creating ambiguities.
Note
Implicit reductions are applied in left-to-right order and expand to the explicit form of the rules.
2.1.4. Context-sensitive semantics¶
We define SIMPL language constructs whose semantics depend on the evaluation context. First we extend the syntax definition of SIMPL with let-expressions:
1 2 3 | context-free syntax
Exp.Let = <let <ID> = <Exp> in <Exp>> {non-assoc}
Exp.Var = <<ID>>
|
This accepts expressions that bind and read variables. An example of a such a program is:
let x = 40 in x + 2
We expect the program above to evaluate to NumV(42) and extend the semantics of SIMPL with the following definitions:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | signature
sort aliases
Env = Map(String, V)
components
E : Env
rules
E |- Let(x, e1, e2) --> v2
where
E |- e1 --> v1;
E {x |--> v1, E} |- e2 --> v2.
E |- Var(x) --> E[x].
|
The signature sort aliases subsection defines Env as an alias for an associative array from String to V. We use this associative array as the evaluation context for variables - variable environment. The signature components subsection defines E as a semantic component of type Env. This labelled component (which in our case holds an environment) will be propagated downwards in the evaluation tree.
Looking at the first rule, it reduces a Let term to a value by first reducing the variable expression in the surrounding environment and then reducing the body expression in the updated environment. The variable environment E is received into the reduction rule together with the Let expression to be reduced, and it is propagated downwards in the evaluation tree of the premises. Updates to the environment are not visible upwards in the evaluation tree. The second rule reduces Var expressions to the value associated with the variable name in the variable environment.
Note
Terms left of the |- symbol are called read-only semantic components.
Although we have extended SIMPL with context-sensitive constructs we do not have to modify the reduction rules which are context-independent. DynSem reduction rules do not need to explicitly propagate semantic components that they do not depend on.
We illustrate the principle of implicit propagation by further extending SIMPL with mutable variable boxes:
1 2 3 4 | context-free syntax
Exp.Box = <box(<Exp>)>
Exp.Unbox = <unbox(<Exp>)>
Exp.Setbox = <setbox(<Exp>, <Exp>)>
|
This accepts programs that use mutable variables. The Box expression allocates a new box on the heap and puts the result of the expression in the box, evaluating to a box value. The Unbox expression reads the value inside the box provided by the argument expression. The Setbox expression puts the value of the second expression inside the box provided by the first expression. For example, a valid program could be:
let b = box(40) in setbox(b, unbox(b) + 2)
We extend the DynSem specification with the following signature and reduction rules for box operations:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | signature
constructors
BoxV: Int -> V
sort aliases
Heap = Map(Int, V)
components
H : Heap
rules
Box(e) :: H --> BoxV(addr) :: Heap {addr |--> v, H'}
where
e :: H --> v :: H';
fresh => addr.
Unbox(e) :: H --> H'[addr] :: H'
where
e :: H --> BoxV(addr) :: H'.
Setbox(box, e) :: H --> v :: Heap {addr |--> v, H''}
where
box :: H --> BoxV(addr) :: H';
e :: H' --> v :: H''.
|
where BoxV is a new SIMPL value representing the address of a box in the heap H. The Box reduces to a BoxV value by reducing the subexpression to a value, obtaining a new unoccupied address using the fresh primitive. It extends the incoming Heap with a new entry for the evaluated expression at the new address. The Unbox rule reduces the subexpression to a box value and looks up the associated value in the H.
Note
Terms to the right side of :: symbol are called read-write semantic components. They are woven through the evaluation tree and updates to them are made visible upwards in the evaluation tree.
Similarly to the addition of the let-expression, extending with a heap structure and mutable variables does not require changing the existing reduction rules. Rules do not have to explicitly mention (or handle) read-write components which they do not depend on.
2.1.5. Conditional semantics¶
We illustrate how to specify the semantics of a conditional language construct by introducing an ifz expression in SIMPL. Extend the syntax definition of SIMPL with the following:
1 2 | context-free syntax
Exp.Ifz = <ifz <Exp> then <Exp> else <Exp>>
|
The ifz expression executes the then expression if the condition expression evaluates to 0, or executes the else expression otherwise. An example of a valid SIMPL program is:
1 2 | let iszero = a -> ifz(a) then 1 else 0
in iszero(42)
|
We extend the semantics with the following DynSem rule:
1 2 3 4 5 6 7 8 9 | rules
Ifz(NumV(ci), e1, e2) --> v
where
case ci of {
0 =>
e1 --> v
otherwise =>
e2 --> v
}.
|
The condition expression is first evaluated to a NumV. The two cases of interest are handled using the case pattern matching premise (Rules).
2.1.6. Semantic libraries using meta-functions¶
To keep reduction rules concise and simple it is useful to introduce layers of abstraction over common semantic operations. For example, in the case of SIMPL we can abstract away from much of the operations that depend on the variable environment and the heap. Instead of directly manipulating the heap and environment in the reduction rules of the SIMPL expressions one can define meta-functions to encapsulate heap and environment operations. The meta-functions introduced can be reused in all places where access to the environment or heap is required.
Note
Meta-functions declarations are 2-in-1 auxiliary constructors and relation declaration used for library abstractions. They benefit from implicit propagation of semantic components just like regular reduction rules. See Signatures of arrows, components and meta-functions for details on how they are declared.
To create the abstractions we first define a module to hold the sort declaration for V and the variable scheme v:
1 2 3 4 5 6 7 8 | module trans/runtime/values
signature
sorts
V
variables
v : V
|
Note
Read about variable schemes in the dynsem_reference_signatures section.
These declarations can be imported in the rest of the specification. We define the environment meta-functions:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | module trans/environment
imports
trans/runtime/values
signature
sort aliases
Env = Map(String, V)
components
E : Env
arrows
bindVar(String, V) --> Env
readVar(String) --> V
rules
E |- bindVar(x, v) --> {x |--> v, E}.
E |- readVar(x) --> E[x].
|
And declare the bindVar and readVar meta-functions which update the environment with a new binding and read the associated value, respectively. Note in the highlighted declaration lines the --> arrow marking the constructor declaration as meta-functions. Similarly, define meta-functions for heap operations:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | module trans/runtime/store
imports
trans/runtime/values
signature
sort aliases
Heap = Map(Int, V)
components
H : Heap
arrows
read(Int) --> V
allocate(V) --> Int
write(Int, V) --> V
rules
read(addr) :: H --> H[addr].
allocate(v) --> addr
where
fresh => addr;
write(addr, v) --> _.
write(addr, v) :: H --> v :: H {addr |--> v, H}.
|
And declare meta-functions allocate, read, write, which create a box, read the contents of a box and update the contents of the box, respectively. Note that since the allocate rule does not access the Heap locally it can be left implicit. We can use the meta-functions to re-specify the semantics of the context-sensitive SIMPL constructs:
1 2 3 4 5 6 | rules
Let(x, v1, e2) --> v2
where
E bindVar(x, v1) |- e2 --> v2.
Var(x) --> readVar(x).
|
By using the semantic abstractions over the environment the rules become more concise and do not depend on specific implementations. Note that because the environment does not have to be explicitly propagated the rules can rely on implicit reductions. The rules above automatically expand to their fully explicated variants. During the expansion first the implicit reductions are lifted:
1 2 3 4 5 6 7 8 9 | rules
Let(x, v1, e2) --> v2
where
bindVar(x, v1) --> E';
E' |- e2 --> v2.
Var(x) --> v
where
readVar(x) --> v.
|
Secondly the semantic components (read-only and read-write) are explicated:
1 2 3 4 5 6 7 8 9 | rules
E |- Let(x, v1, e2) --> v2
where
E |- bindVar(x, v1) --> E';
E' |- e2 --> v2.
E |- Var(x) --> v
where
E |- readVar(x) --> v.
|
Note
The performance of derived interpreters is not adversely affected by the introduction and use of meta-functions.
Rules for boxes can be re-specified in a similar way to those for environments:
1 2 3 4 5 6 | rules
Box(v) --> BoxV(allocate(v)).
Unbox(BoxV(addr)) --> read(addr).
Setbox(BoxV(addr), v) --> write(addr,v).
|
2.1.7. Semantics of functions¶
We grow SIMPL with functions. Functions will be first class citizens SIMPL but will only take a single argument (will be unary). We define syntax for function declaration and application:
1 2 3 | context-free syntax
Exp.Fun = [[ID] -> [Exp]]
Exp.App = <<Exp>(<Exp>)> {left}
|
Now programs such as the following are syntactically correct in SIMPL:
let sum = a -> b -> a + b
in sum(40)(2)
From an execution perspective we expect the above program to evaluate to NumV(42) by first applying function sum to number 40 which evaluates to a function which is applied to number 2. Functions are only associated to names via the let-expression, so annonymous functions literals are allowed. The program below is equivalent to the program above:
(a -> b -> a + b)(40)(2)
From a dynamic semantics point of view we add a new type of value - ClosV - which closes a function body over its declaration environment. A function application reduces the function expression to a ClosV and the application of the closure body to the argument:
1 2 3 4 5 6 7 8 9 10 11 | signature
constructors
ClosV: String * Exp * Env -> V
rules
E |- Fun(x, e) --> ClosV(x, e, E).
App(ClosV(x, e, E), v1) --> v2
where
E |- bindVar(x, v1) --> E';
E' |- e --> v2.
|
2.1.8. Get ready for interpretation¶
To get a functioning interpreter derived from a DynSem specification one has to go through the following steps:
A reduction entry-point¶
The SIMPL interpreter must have a clearly defined entry point. The entry point is a reduction rule over a relation named -init->. The relation named -init-> should satisfy all semantic components of the arrows it applies. By default -init-> is the relation invoked by the interpreter at startup. First we extend the syntax definition with a constructor for the top-level of a program:
1 2 3 4 5 | context-free start-symbols
Prog
context-free syntax
Prog.Program = Exp
|
Term of sort Prog are top-level terms in SIMPL and reduction of a program should start at the only one possible - Program.
1 2 3 4 5 6 7 8 | signature
arrows
Prog -init-> V
rules
Program(e) -init-> v
where
E {} |- e :: H {} --> v :: H _.
|
We extend the DynSem specification with a declaration of the arrow -init-> reducing terms of sort Prog to a value. Program is the only term of sort Prog and we specify its reduction to value. This reduction rule introduces initial values for the variable environment E and for the heap H.
Configure the interpreter generator¶
To configure the interpreter generator with the specifics of SIMPL you will need a dynsem.properties file:
Note
The dynsem.properties file must be located in the root directory of the SIMPL language project, not the interpreter project
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | # the name of the language. may not contain hyphens
source.langname = simpl
# version of this language
source.version = 0.1
# start symbol to use for parsing programs in this language
source.startsymbol = Prog
# constructor name/arity of reduction entry point
source.initconstructor.name = Program
source.initconstructor.arity = 1
# path to interpreter project, absolute or relative to the language project
project.path = ../simpl.interpreter/
# (optional) enable/disable creation of the target project
project.create = true
# (optional) enable/disable cleaning of the target project before writing files
project.clean = true
# groupid & artifactid for the interpreter project
project.groupid = org.metaborg
project.artifactid = simpl.interpreter
# package name for manually implemented interpreter nodes
project.nativepackage = simpl.interpreter.natives
|
The first fragment (lines 1-3) configures the language name, a version identifier and the MIME-TYPE. Line 5 configures the path to the parse table for SIMPL, relative to the project, which will be copied into the interpreter project. Line 6 configures the start symbol used to parse SIMPL programs and it has to be one of the start symbols specified in the syntax definition. Lines 7-8 specify the constructor name and arity to be used as the entry point for the evaluation. It is expected that an -init-> rule is declared for this term. For SIMPL the top-level term and rule are the ones defined in A reduction entry-point.
The third fragment (lines 10-15) sets parameters for the target interpreted project. project.path gives the path to the interpreter project. This must be a path relative to the language project, in this case to the SIMPL project. The project.clean flag indicates whether the target generation directory should be recursively removed (clean compilation target) before generation. If this property is not mentioned in dynsem.properties, it defaults to false. For a detailed explanation of all valid properties consult the Configuration file reference.
Generate interpreter components¶
An interpreter derived from a DynSem specification relies on components that are generated from the specification. This generation project happens on-demand. Ensure that the SIMPL language project is built and that you have the SIMPL interpreter project open in the Eclipse workspace. Open the top-level DynSem specification file - simpl.ds - and select . Observe that files have been placed into the SIMPL interpreter project:

The src/main/java directory contains the SIMPL-specific generated term library. The src/main/resources directory contains the SIMPL parse table (parsetable.tbl) and an interpretable form of the DynSem specification (specification.aterm).
Note
At this stage it is normal that the project contains Java errors about the missing simpl.interpreter.natives package. We will populate this package with native operations (see Call into Java code). If other errors are reported make sure you have enabled and configured annotation processing:
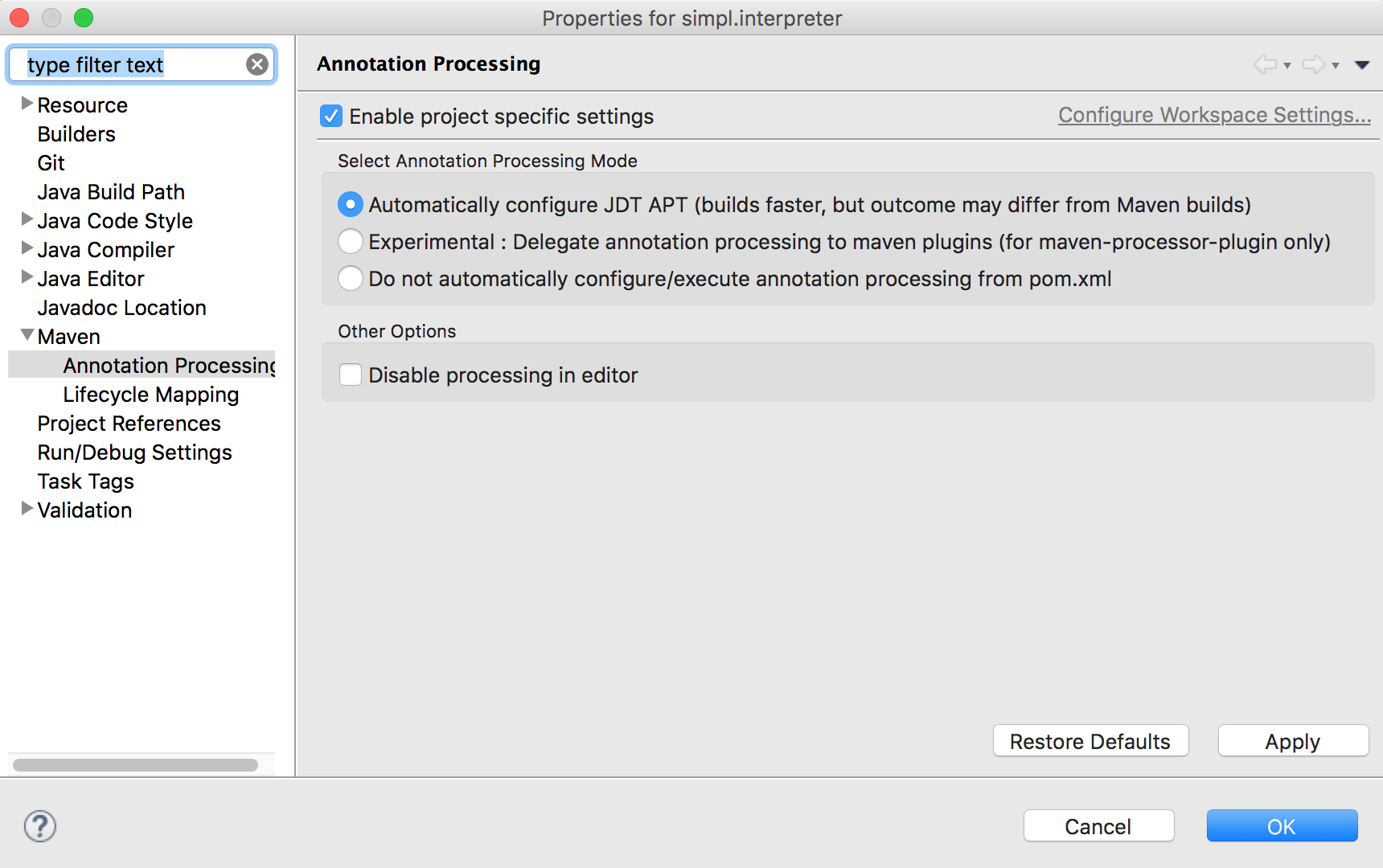
Warning
If the entry is not available it means you propbably do not have the M2E-APT Eclipse plugin installed. Install it from the Eclipse Marketplace and try again to configure the project by selecting in the window pane opened by selecting .
2.1.9. Call into Java code¶
Many times a semantics for a language will depend on operations whose specification/implementation will reside outside of the formal specification. In the case of the SIMPL language such operation are the conversion of a string representation of a number to a number literal, arithmetic operations, and the fresh address generator. More complex languages will require interactions with existent systems such as application of library functions. DynSem sepcifications can interact with specification-external (native) operations by means of native operators. Although we have used native operators for arithmetic operations in SIMPL, this guide has so far ommitted their signature declaration:
1 2 3 4 5 6 | signature
native operators
parseI: String -> Int
addI: Int * Int -> Int
subI: Int * Int -> Int
mulI: Int * Int -> Int
|
Line 3 declares the parseI native operator which takes one argument of type String and produces an Int. For a detailed explanation of the native operators signature section consult the Term signatures page.
We now provide an implementation for parseI and for addI. Create the package simpl.interpreter.natives. This package has to be same as the one specified in the target.nativepackage property in Configure the interpreter generator. Inside the package create an abstract class named `parseI_1:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | package simpl.interpreter.natives;
import org.metaborg.meta.lang.dynsem.interpreter.nodes.building.TermBuild;
import com.oracle.truffle.api.dsl.NodeChild;
import com.oracle.truffle.api.dsl.Specialization;
import com.oracle.truffle.api.source.SourceSection;
@NodeChild(value = "stringbuild", type = TermBuild.class)
public abstract class parseI_1 extends TermBuild {
public parseI_1(SourceSection source) {
super(source);
}
@Specialization
public int doInt(String s) {
return Integer.parseInt(s);
}
public static TermBuild create(SourceSection source, TermBuild stringbuild) {
return parseI_1NodeGen.create(source, stringbuild);
}
}
|
The class name parseI_1 is required: it’s the name of the constructor (parseI) followed by _ and its arity (1). The class extends DynSem’s TermBuild class which corresponds to DynSem fragments that construct terms. The @NodeChild annotation is a Truffle annotation declaring a child to our class, named stringbuild of the TermBuild type. This child corresponds to the sole argument of the parseI constructor.
The class is abstract as we rely on Truffle’s annotation processor to generate a concrete class named parseI_1NodeGen. The method declaration at line 17 implements the business logic of the parseI node. It receives one argument corresponding to the evaluated stringbuild child and relies on the Java standard library to parse the string to an integer.
The method declared on line 21 is a factory method instantiating the generated subclass of parseI_1. The generated language specific library uses this method to obtain instances of the parseI_1 term build.
In a similar way create an implementation for the addI native operator with arity 2:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | package simpl.interpreter.natives;
import org.metaborg.meta.lang.dynsem.interpreter.nodes.building.TermBuild;
import com.oracle.truffle.api.dsl.NodeChild;
import com.oracle.truffle.api.dsl.NodeChildren;
import com.oracle.truffle.api.dsl.Specialization;
import com.oracle.truffle.api.source.SourceSection;
@NodeChildren({ @NodeChild(value = "left", type = TermBuild.class),
@NodeChild(value = "right", type = TermBuild.class) })
public abstract class addI_2 extends TermBuild {
public addI_2(SourceSection source) {
super(source);
}
@Specialization
public int doInt(int left, int right) {
return left + right;
}
public static TermBuild create(SourceSection source, TermBuild left,
TermBuild right) {
return addI_2NodeGen.create(source, left, right);
}
}
|
The significant difference to parseI is that addI has two children. Using the @NodeChildren Truffle annotation multiple child fields can be specified, in this case left and right. Both of the children are expected to evaluate to integers, expectation made explicit in the method declaration of line 19. The factory method of line 23 receives two children arguments, reflecting the arity of the addI constructor. The SIMPL interpreter project should have no errors once all required native operators are defined.
Note
The implementation for the other native operators used by SIMPL can be found in the repository at tags/native-operators.
2.1.10. Run a program¶
After following through the previous steps the SIMPL interpreter is ready to be imported into the workspace and begin to evaluate programs. Before continuing import the generated interpreter project into the workspace by .
Create a simple program and save it as simple/examples/ex1.smpl:
let sum = a -> b -> a + b
in sum(40)(2)
A launch configuration for the interpreter project has automatically been generated. It can evaluate files that are selected or open in Eclipse. Either select the ex1.smpl file in the Package Explorer or open it in the editor. With focus on the example file, evaluate it by selecting , select in the left hand side pane and select the simpl launch configuration.
Press . Observe the result of evaluating the program in the Console view.